אפלטון קישר אותה לאדמה, קפלר טען שאפשר לדעת באמצעותה את מבנה מערכת השמש, והיום מדענים גילו כי הקובייה היא מבנה היסוד שאליו מתפרקים אובייקטים בטבע, מסלעים ועד קרח. האם חוט אחד קושר בין כל הסיפורים?

שחקני שש-בש ידועים בדרכים היצירתיות להפיח מזל בקוביות המשחק שלהם. נשיפת רוח, נשיקה, הטלת מסובסבת, דימוי המספרים בעיני הדמיון, כל אחד ומה שעובד לו (מדי פעם). התכונות הגיאומטריות של הקובייה הופכות אותה לאחת הצורות האידיאליות ליצירת תוצאות אקראיות ולכן היא קשורה אצלנו למזל. אבל אירוני למדי, אותן התכונות הן מתמטיות, סטטיסטיות וניתנות לחיזוי. עד כדי-כך, שלאורך הדורות ניסו כמה מהמוחות הגדולים בהיסטוריה להסביר באמצעותה את יסודות מבנה היקום, כפי שהיה מוכר לבני כל תקופה.

אנחנו לא יודעים איפה בדיוק התחיל הסיפור של הקובייה. בטבע הצורה קיימת רק ברמה המולקולרית, כך שסביר מאוד להניח שהאדם לא פגש קוביות מושלמות בעצמים סביבו. ככל שזה נוגע לאדם, עד ימי המיקרוסקופ הייתה הקובייה יותר בגדר רעיון מופשט, אידיאה של המרחב. או, אפשר לומר, ביטוי מתמטי שאפשר ליצור, אבל קשה עד בלתי אפשרי למצוא. וכמו בהרבה מהרעיונות המופשטים של המתמטיקה, אנחנו יכולים להרחיק עד יוון העתיקה כדי למצוא התייחסות מתועדת.

אפלטון חיפש אחר הצורות האידיאיות של היקום

כדי להבין את הרקע לעיסוק המוקדם בקובייה צריך להכיר את המשפחה שלה. קובייה היא מה שמכונה פאון משוכלל, צורת תלת ממדית שכל פניה זהים ובכל קודקוד נפגש מספר שווה של צלעות. לקובייה 4 אחיות נוספות: ארבעון, תמניון, תריסרון ועשרימון. יחד עם הקובייה מדובר במשפחה בת 5 נפשות. בכל צירופי הגיאומטריה האפשריים, אין עוד צורה שעונה להגדרות האלה. נדירותן של תכונות אלה אולי הציתה בחוקרים את האינטואיציה שיש מה לנבור פה.

עבור אפלטון, שהיה בעל נטייה חזקה לתאר את המופשט והיסודי, התכונות הללו היו כה בסיסיות שהוא קישר אותן למבנה היקום. למעשה, באנגלית הצורות שאנו מכנים פאונים משוכללים, קרויות על שמו – Platonic solids. את התיאוריה שלו פרש בדיאלוג טימאוס ובו הוא מפרט כל צורה ויסוד מבין 4 היסודות שאליו היא קשורה. מייקל סטיבנס, יוטיובר פופולארי מאוד בתחום המדע, מסביר בערוץ DING כי את הארבעון קישר אפלטון ליסוד אש, את התמניון לאוויר, את העשרימון למים ואת התריסרון לקונסטלציות הכוכבים. יותר מאוחר בא אריסטו וקישר את הצורה ליסוד אתר. היסוד הנותר מבין הארבעה הוא האדמה, ואותה קישר אפלטון לקובייה. מדוע? אולי מפני ש"ניתן לערום ולאזן אותה בצורה נאה ויציבה על עצמה", סטיבנס מפרשן את אפלטון.

ההיגיון של הפילוסוף היווני לא הכזיב; משהו באינטואיציה שלו לגבי הקשר בין אדמה וקוביות לא היה רחוק מאוד מהאמת. באנציקלופדיה של National Geographic מוסבר כי חלק מהסלעים המותמרים נוצרים כתוצאה מלחץ נמוך יחסית, המשטח מינרלים לשכבות ועורם אותם אלה על גבי אלה. אומנם לא בדיוק קובייה, ורק אחד מתהליכים רבים של היווצרות סלעים, אבל חכו, אנחנו מתקרבים.

בינתיים חולפות אלפיים שנים בקירוב, שבהן כל מיני דברים קרו בחקר היקום, רובם הגדול נחשב בימינו למעשיות. אבל אז הגיעה החבורה של קופרניקוס, גליליאו וקפלר, שאומנם לא באמת היו חבורה (קופרניקוס נפטר שנים ספורות בטרם נולדו שני האחרים), אבל עבודתם המצטברת נחשבת לציר מפנה במדע האסטרונומיה.

"דמיינו בובת מטריושקה שבגרעינה פלנטה עטופה בפאון משוכלל, וסביבה שכבות נוספות של פלנטה-פאון וכך הלאה בהתאם לגודל הפלנטות, כשהצמד העוטף את כולם הוא קובייה וסביבה שבתאי. הסידור הזה, מסביר פרופסור וילצ'ק, 'על אף שלא היה מדויק, היה קרוב מספיק כדי לשכנע את קפלר כי ייתכן שהוא על המסלול הנכון'"

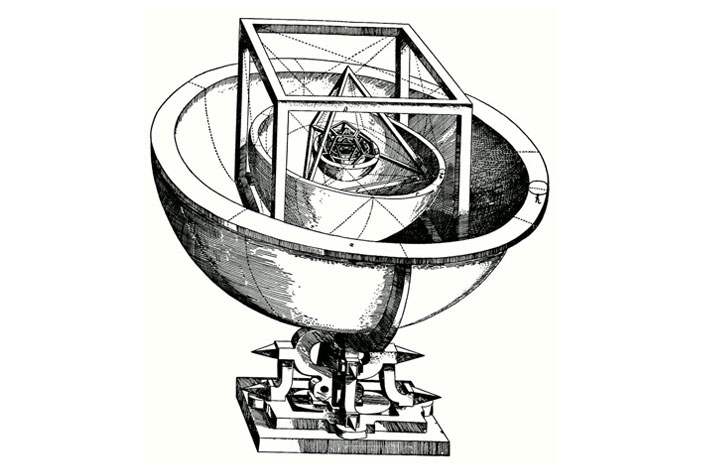
יוהאנס קפלר גילה סקרנות יתרה במחשבה האפלטונית והוציא מעליית הגג את תיאוריית הפאונים המשוכללים כדי לעשות לה רה-אורגניזציה. הפיזיקאי זוכה פרס הנובל פרופסור פרנק וילצ'ק, מסביר באתר של הסדרה המדעית Nova מבית PBS, כי קפלר ניסה לתאר באמצעות הצורות את הסדר, היחסים והמרחקים בין הפלנטות של מערכת השמש שלנו. הימים ימי המהפכה המדעית ולמדע מוכרים 6 פלנטות בלבד: ארץ, חמה, נוגה, מאדים, צדק ושבתאי. מלבד כדור הארץ, שממנו נחקרת המערכת, אנו נשארים עם 5 פלנטות, כמניין הפאונים המשוכללים.

במילים פשוטות, האסטרונום טען כי אם לוקחים פלנטה אחר פלנטה ועוטפים אותה בפאונים משוכללים, מתקבל היחס המתמטי שבין גרמי השמיים והשמש. דמיינו בובת מטריושקה שבגרעינה פלנטה עטופה בפאון משוכלל, וסביבה שכבות נוספות של פלנטה-פאון וכך הלאה בהתאם לגודל הפלנטות, כשהצמד העוטף את כולם הוא קובייה וסביבה שבתאי. הסידור הזה, מסביר פרופסור וילצ'ק, "על אף שלא היה מדויק, היה קרוב מספיק כדי לשכנע את קפלר כי ייתכן שהוא על המסלול הנכון. מעודד, הוא יצא, באומץ, להוכיח זאת". בסופו של דבר אכן קפלר גילה כי היחסים בין הפאונים והפלנטות אינם מדויקים, אבל ניסיונו להוכיח זאת בפירוש קירב אותו לתיאור המדויק ביותר של מערכת השמש עד זמנו. החוקים שניסח בהמשך ובעקבות התיאוריה האפלטונית מהווים את יסוד האסטרונומיה עד ימינו.

העולם בנוי מקוביות… בממוצע

בימינו, לקובייה אין כל-כך מקום בין גרמי השמיים, אבל בגלגול משונה של ההיסטוריה היא חזרה במובן מסוים למקורה הארצי-אפלטוני. זה קרה, כפי שמיטיב לתאר ג'ושוע סוקול במגזין Quanta, "ביום סתווי מתון ב-2016". באותו יום המתיק המתמטיקאי ההונגרי גאבור דומוקס סוד עם עמיתו, הגיאופיזיקאי דאגלס ג'רולמאק. בעוד השניים מהלכים על חצץ בחצר ביתו של האחרון, מספר סוקול, פתח דומוקס ושאל: "כמה פאות יש לכל אחת מהאבנים הללו? מה אם אומר לך שהמספר תמיד יהיה באזור השש?"

"לאחר מכן", ממשיך סוקול, "הוא שאל שאלה גדולה יותר […] מה אם העולם עשוי מקוביות?"

מודל מערכת השמש של קפלר, המבוסס על תיאוריית הפאונים של אפלטון. מקור: wikipedia

קדמה לפגישה הזו עבודה מתמטית מאומצת של דומוקס, שמידת הרחמים מחייבת להשאיר לחובבי הז'אנר. אבל סופה היה נוסחה המוכיחה כי "כל סלע שנשבר באופן אקראי, יתפרק לצורות בעלות ממוצע של שש פאות ושמונה קודקודים". במילים אחרות – קוביות.

אחרי התיאוריה הגיעה השעה לבדוק מה קורה בפועל. בניסויי מעבדה של ריסוק סלעים התברר כי דולומיט, גבס, ואבן גיר, כולם מתפוררים לקוביות בממוצע. בהמשך נמצא שגם שכבות קרח באלסקה נסדקות לפי דפוס שתואם את הנוסחה, רק בהמרה לדו-ממד, וכך גם לגבי גושי גרניט. אבל זה לא הספיק לשני המדענים. הסיפור היה כה מוזר, בייחוד עבור הגיאופיזיקאי שבא במגע עם צורות הטבע ומכיר את הכאוס השורר בו, שהוא יצא לחפש דרך להפריך אותו. לא מטעם פסול, אלא כדי לחזק ולאמת את התיאוריה.

"בעוד השניים מהלכים על חצץ בחצר ביתו של האחרון, פתח דומוקס ושאל: 'כמה פאות יש לכל אחת מהאבנים הללו? מה אם אומר לך שהמספר תמיד יהיה באזור השש?' לאחר מכן הוא שאל שאלה גדולה יותר: מה אם העולם עשוי מקוביות?"

הם מצאו מספר מקרים כאלה, אבל בהם הכוחות הפועלים על החומר מושכים החוצה, ולא דוחפים פנימה כמו בשבירה של סלע. עם הצטברות הנתונים גדל הביטחון של השניים והם החליטו לבדוק תופעה גדולה בהרבה: האם הלוחות הטקטוניים של כדור הארץ נענים לנוסחה.

במבט ראשון נראה היה להם כי אכן, הלוחות אכן מחולקים לצורות שתואמות את גרסת הדו-ממד של הנוסחה. כשבדקו, ממוצע הקודקודים היה 5.77. הדפוס הדו-ממדי היה אמור לספק 6 קודקודים (בשונה מ-8 הקודקודים של הקובייה התלת ממדית). "עבור גיאופיזיקאי זה היה קרוב מספיק כדי לחגוג. עבור מתמטיקאי, לא כל-כך". דומוקס, אם כן, המשיך לשבור את הראש על הבעיה, עד שזה היכה בו. כדור הארץ עגול, ואילו יתר התופעות נבדקו על מישורים שטוחים. בשקלול צורתו העגולה של שטח פני כדור הארץ, הממוצע שקיבל דומוקס היה 5.77 קודקודים. הלוחות המצפים את כדור הארץ, כמו גם הסלעים שממנו הוא מורכב ותופעות טבע נוספות, כולם נשברים לפי דפוס דומה, עם ההתאמות הדרושות בין דו לתלת ממד.

כאוס שמסתיר שלמות סימטרית

ג'רולמאק, שהיה סקפטי בהתחלה לגבי העניין, השתכנע מהעקביות של המספרים ואף למד לחבב את הקשר של התיאוריה לאפלטון. "זוהי הדוגמה הישירה ביותר [לתיאוריה האפלטונית] שאפשר לחשוב עליה", אמר. "הממוצע הסטטיסטי של כל התצפיות האלה הוא קובייה, אבל הקובייה אף פעם לא קיימת".

כאמור, בטבע אפשר למצוא קוביות ברמת המולקולות, כמו במקרה של המינרל פיריט. אבל זה מקרה נדיר מאוד, ולרוב התיאור של ג'רולמאק קולע. התשתית הרעיונית של העולם, ואולי גם של היקום, עשויה להיות מורכבת מגיאומטריה של סימטריה מושלמת, אבל הביטויים שלה יכולים להתגלם באלף אלפי ורסיות של הרעיון. כמו בקובייה, סטטיסטיקה יכולה לעזור לנו לשחזר את הצורה המקורית ולהבין את המספרים, אבל בפועל הטבע נראה לנו אקראי ומגוון. ואולי מזל שכך.

תמונת כותרת: Logan Baker Visuals / shutterstock

כתבות נוספות שעשויות לעניין אותך:

0 ו-1 מגדירים את עצם קיומנו במובן עמוק בהרבה מהמהפכה הדיגיטלית

בין קן נמלים לרשת הקוסמית – מדענים חושפים את מסתרי המוח במקומות משונים

האופי החמקמק של יופי – אומנים, פיזיקאים ופילוסופים מסבירים כי סימטריה זה לא הכול

עוד מרדיו מהות החיים:

חיים ברטרו – נחיתת האדם על הירח